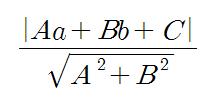할 일이 없다보니, 전에 몰두하던 점과 직선 사이의 거리를 구하는 것에 대해 다시 한번 생각해 보게 되었습니다.
그러다 점과 직선사이의 거리 공식을 유도하는 다른 방법을 알게 되었습니다.
한번 정리해 보겠습니다.
전에 공식을 유도했던 방식은 선 밖의 점과 최단거리에 있는 직선 위의 점을 구해서 두점사이의 거리를 구하는 것 이었습니다.
제가 이번에 생각해낸 방식은 기하학적인 방식을 이용하는 것 입니다.
먼저 전과 같이 점과 선을 설정합니다.
x축과 평행한 선분ER, y축과 평행한 선분QR, 그리고 주어진 직선과 직교하는 선분 WR을 그려넣었습니다.
이렇게 하면 선분들이 서로 만나는 점들이 4개 생기는데, 이 점들에 문자를 하나씩 대응해 놓았습니다.
이제 여기서 선분WR의 길이를 구하면 되는 것입니다.
그림에서 만들어진 삼각형QER의 넓이를 구하는 방법은 2가지가 있습니다.
첫번째 방법은, 선분ER*선분QR*1/2
두번째 방법은, 선분QE*선분WR*1/2
여기서 "선분ER*선분QR = 선분QE*선분WR"이 됨을 알 수 있습니다.
선분의 길이를 주어진 직선의 방정식(Ax+By+C=0)과 점(a,b)로 표현하여 선분ER을 구해보면
전에 구했었던 공식을 보다 쉽게 구할 수 있습니다.
이 과정을 밟으면서 알게 된 것이 있습니다.
저는 전부터 어떤 직선의 방정식에 선 밖의 점을 대입해 나오는 값의 의미가 과연 무엇일까?하고 궁금해해 왔습니다.
두번째 공식유도 방식을 생각해 내면서 이에 대한 답을 어느정도 얻게 되었습니다.
그 값(Aa+Bb+C)은 위에 그린 그림에서 선분ER, 선분QR, 선분QE, 선분WR과 모두 비례한다는 것입니다.
경우에 따라서는 그 값이 서로 일치할 수도 있습니다.
'글쓰기' 카테고리의 다른 글
| 안철수•박경철 희망공감 청춘콘서트-춘천 (4) | 2011.07.24 |
|---|---|
| 춘천 원창고개 금병산 (0) | 2011.06.06 |
| 삼성과 MB정권과 민주화정권, 어떻게 봐야할까? - 장하준의 시선이 필요하다. (0) | 2010.12.31 |
| 청량리역 코코이찌방야 카레전문점 (0) | 2010.12.30 |
| 청량리 롯데백화점 카페파스쿠찌(CAFFE PASCUCCI) (0) | 2010.12.29 |
| 경춘선 전철을 타다 - 새로생긴 남춘천역 사진 (0) | 2010.12.28 |
| 우울할땐 LG유플러스 고객센터에 전화를 걸어보자. (0) | 2010.12.22 |
| 레이저로 점빼기 시술했습니다. (0) | 2010.12.14 |
| 컴퓨터활용능력 1급 필기합격 수기 - 기출문제풀이가 중요 (10) | 2010.04.11 |
| 점과 직선 사이의 거리 (4) | 2008.11.20 |